Voyage dans les réseaux neuronaux (2e partie) : les neurones logiques
sur
Dans la première partie de cette série d'articles, nous avons découvert comment les chercheurs ont lentement approché les caractéristiques fonctionnelles du neurone. La véritable percée des neurones artificiels est venue du perceptron multicouche (MLP) et de l'utilisation de la rétropropagation pour lui apprendre à classer les entrées. En réalisant un MLP à partir de zéro dans Processing, nous avons également montré comment il fonctionnait et ajustait ses poids pour apprendre. Ici, nous reprenons les expériences du passé pour apprendre à notre réseau neuronal le fonctionnement des portes logiques et vérifier si notre perceptron multicouche (MLP) est capable d'apprendre la fonction XOR (OU exclusif).
Nous disposons d'une classe Neural flexible pour implémenter un MLP qui pourra être éventuellement incorporé dans un projet Processing. Pour autant, les exemples examinés jusqu'à présent n'ont pas donné grand-chose. Ils confirment simplement le calcul correct de la progression avant et la façon dont la rétropropagation ajuste les poids du réseau pour apprendre une tâche donnée.
Le moment est maintenant venu d'appliquer ces connaissances à une tâche réelle, celle-là même qui a été étudiée lors des premières recherches sur les unités logiques à seuil (TLU) de McCulloch-Pitts : la mise en œuvre de la logique. Comme nous l'avons déjà découvert, notre MLP devrait résoudre facilement des problèmes linéairement séparables tels que les fonctions ET et OU. De plus, il devrait également être capable de résoudre la fonction OU exclusif, ce que ne pouvaient pas faire les TLU et les premiers neurones artificiels. Au cours de ce voyage, nous examinerons également comment ces réseaux apprennent grâce à une implémentation visuelle du réseau neuronal. Nous étudierons également l'impact du taux d'apprentissage choisi sur l'erreur de sortie pendant l'apprentissage.
ET
Si un réseau neuronal peut apprendre à reproduire la fonction ET, il n'opère pas tout à fait de la même manière. Ce que nous faisons en fait, c'est appliquer des entrées à un réseau qui a appris la fonction ET et lui demander : « Dans quelle mesure es-tu sûr que cette combinaison d'entrées est le modèle auquel nous attribuons un 1 ? ».
Pour le démontrer, un exemple de projet a été préparé et est disponible dans le référentiel GitHub dans le dossier /processing/and/and.pde. Il doit être ouvert à l’aide de Processing.
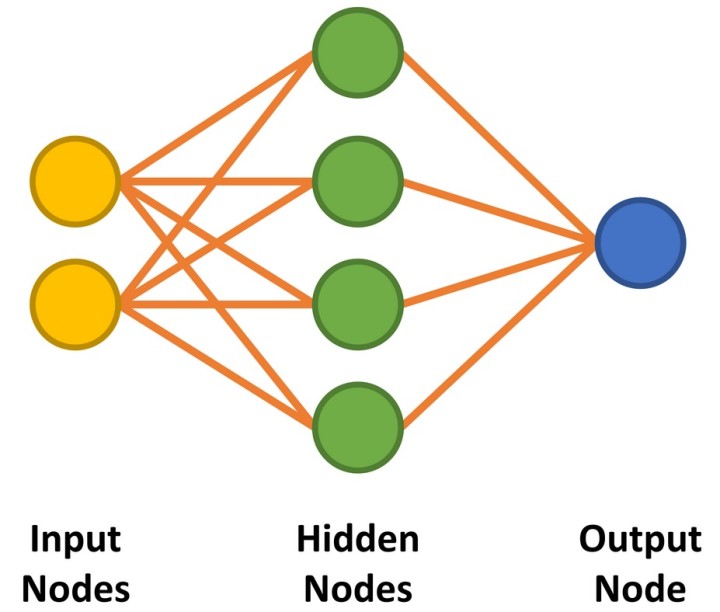
Notre réseau neuronal comporte deux entrées et une seule sortie pour répondre aux caractéristiques d'une porte ET à deux entrées. Entre les nœuds d'entrée et de sortie, nous implémentons quatre nœuds cachés (figure 1). Nous aborderons plus tard la manière de déterminer le nombre de nœuds cachés requis. Le code permettant de préparer le réseau est présenté dans le listage 1.

L'objectif est d'entraîner le réseau à reconnaître le motif '11' sur les entrées. Nous voulons également nous assurer que les alternatives '00', '01' et '10' ne dépassent pas notre seuil de classification. Pendant l'apprentissage du réseau, nous appliquerons les stimuli et les résultats attendus indiqués dans le tableau 1.
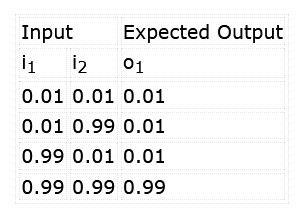
Notez que, plutôt que de travailler avec des niveaux logiques, ces réseaux fonctionnent avec des valeurs décimales. Dans ce cas, un 1 est entré comme 0,99 (presque 1), tandis qu'un 0 est entré comme 0,01 (presque 0). La sortie sera également comprise entre 0,0 et 1,0. Nous pouvons voir cela comme un niveau de confiance dans la correspondance entre les entrées et la classification apprise : nous avons, par exemple, 96,7 % de confiance que les deux entrées sont à '1', plutôt que d’avoir une sortie logique tranchée 0/1 d'une porte ET réelle.
Nous pouvons commencer par déterminer si ce réseau nouvellement créé « sait » quelque chose en lui appliquant quelques entrées et en lui demandant ce qu'il a en sortie. N'oubliez pas que les résultats produits seront différents à chaque fois, car le constructeur applique des valeurs aléatoires aux poids.
Le code ci-dessous donne la réponse du réseau pour les entrées '11' et '00'. Il est fort probable que le résultat pour '11' soit proche de 0,99, alors que le résultat pour '00' sera beaucoup plus grand que le 0,01 espéré :
// Vérifier la sortie de la fonction ET pour une entrée 00
network.setInputNode(0, 0.01);
network.setInputNode(1, 0.01);
network.calculateOutput();
println(“For 00 input, output is: ”, network.getOutputNode(0));
// Vérifier la sortie de la fonction ET pour une entrée 11
network.setInputNode(0, 0.99);
network.setInputNode(1, 0.99);
network.calculateOutput();
println(“For 11 input, output is: ”, network.getOutputNode(0));
La sortie obtenue au cours du test est la suivante :
For 00 input, output is: 0.7490413
For 11 input, output is: 0.80063045
Nous voyons ici que lorsque nous appliquons 0,99 aux deux entrées, le réseau neuronal pense que l'entrée est '1 ET 1' avec un niveau de confiance de 0,8006, ce qui correspond à 80,06 %. Ce n'est pas si mal à ce stade. Cependant, en appliquant 0,01 aux deux entrées, le réseau neuronal a un niveau de confiance de 0,7490 (74,90 %) que l'entrée est '1 ET 1'. Nous sommes encore loin de ce que nous voulons, soit une valeur proche de 0 %.
Pour apprendre au réseau comment fonctionne une fonction ET, un entraînement est nécessaire. Pour ce faire, il faut définir les entrées et la sortie souhaitée de manière appropriée pour les quatre cas (00, 01, 10 et 11, et 0, 0, 0 et 1 respectivement) et appeler la méthode calculateOuput() en activant l'apprentissage après chaque modification. Cette opération est effectuée dans une boucle comme suit :
while (/* learning the AND function */) {
// Learn 0 AND 0 = 0
network.setInputNode(0, 0.01);
network.setInputNode(1, 0.01);
network.setOutputNodeDesired(0, 0.01);
network.calculateOutput();
// Learn 0 AND 1 = 0 … Learn 1 AND 0 = 0
// Learn 1 AND 1 = 1
network.setInputNode(0, 0.99);
network.setInputNode(1, 0.99);
network.setOutputNodeDesired(0, 0.99);
network.calculateOutput();
}
network.turnLearningOff();
La décision d'arrêter l'entraînement du réseau peut être déterminée de plusieurs façons. Dans cet exemple, chaque cycle d'apprentissage est considéré comme une époque. Il est possible d’arrêter l'apprentissage lorsqu'un nombre spécifique d'époques, par exemple 10 000, est atteint. Il est également possible d'éliminer l'erreur dans la sortie. Une fois qu'il a atteint un niveau inférieur à 0,01 %, par exemple, le réseau peut être considéré comme suffisamment précis pour la tâche de classification en cours.
À noter qu'un MLP ne converge pas toujours vers le résultat souhaité. Il est possible que la combinaison des poids et des poids de biais sélectionnés soit malchanceuse. Il se peut également que la configuration du MLP ne soit pas capable d'apprendre votre tâche, probablement en raison d'un nombre trop élevé ou trop faible de nœuds cachés. Ici, il n'y a pas de règles - le nombre approprié de nœuds, les poids de départ et les biais ne peuvent être déterminés que par essai et erreur ou par expérience. Pour cet exemple, quatre nœuds cachés ont été choisis car l'apprentissage porte sur quatre états. L'idée était que chaque nœud caché apprendrait un état.
Il convient également de noter que l'apprentissage doit se faire par lots, c'est-à-dire que l'ensemble des données d'apprentissage doivent être parcourues du début à la fin, de manière répétée. Si '0 ET 0 = 0' est appliqué de manière répétée au cours de plusieurs milliers de cycles, le réseau s'oriente vers ce résultat et il devient presque impossible d'entraîner les données restantes.
La mise en œuvre de base étant traitée, nous pouvons maintenant examiner de plus près l'exemple d'entraînement du réseau pour apprendre la fonction ET. Pour mieux montrer comment les réseaux neuronaux apprennent, le réseau est visualisé dans l'application pendant l'apprentissage et, ensuite, au cours du fonctionnement.
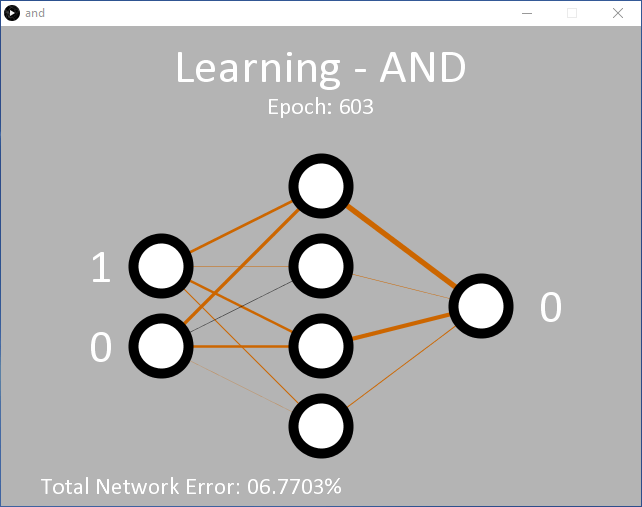
En cliquant sur 'Run' (Exécuter), on obtient la sortie représentée sur la figure 2 (capture d'écran). Au départ, l'application est en mode apprentissage et enseigne au réseau la sortie attendue pour une fonction ET, pour les deux entrées. Les nœuds d'entrée se trouvent à gauche. Pendant l'apprentissage, les valeurs d'entrée passent rapidement entre les niveaux logiques 0 et 1. À droite, se trouve le nœud de sortie unique. Initialement, il est à 0. La décision de produire un 1 en sortie n'est prise que si le nœud de sortie donne un niveau de confiance de plus de 90 % pour les deux entrées à 1. Sinon, un 0 est émis. Cette décision est prise entre les lignes 341 et 346 dans and.pde.
// Output Node Text
if (network.getOutputNode(0) > 0.9) {
text("1", 550, 280);
} else {
text("0", 550, 280);
}
Au départ, la sortie reste à 0 car le niveau de confiance de 90 % n'a pas encore été atteint. Après environ 5 000 époques, la valeur de sortie devrait commencer à osciller entre 0 et 1, ce qui prouve que le réseau a commencé à classifier avec succès que l'entrée '11' doit produire un '1'. À ce stade, l'erreur totale du réseau est d'environ 0,15 %. Si cela ne se produit pas, il est probable que le réseau s'est bloqué et qu'il ne pourra pas apprendre cette fois-ci.
Au fur et à mesure que le réseau apprend, les poids entre les nœuds sont affichés sous forme de lignes d'épaisseur et de couleur variables. Plus la ligne est épaisse, plus la valeur est grande. Les lignes noires indiquent des nombres positifs, tandis que les lignes marron indiquent des nombres négatifs.
Chaque fois que le code est exécuté, les lignes seront différentes. Vous remarquerez cependant qu'un modèle se développe. Deux nœuds cachés ont toujours une ligne marron et une ligne noire ; un nœud caché a deux lignes noires ; et un nœud caché a deux lignes marron. Les lignes entre les nœuds cachés et le nœud de sortie se conformeront également à un modèle, la seule ligne noire émanant du nœud avec deux lignes de poids noires entrantes.
Il s'agit d'un aperçu intéressant car il montre comment le réseau a appris la fonction ET. Le '00' en entrée se convertit facilement en un 0 à la sortie, tout comme le '11' en un 1. Pour les combinaisons '01' et '10', il semble que les 0 fassent le plus gros du travail en poussant la sortie vers 0.
L'application est programmée pour arrêter l'apprentissage lorsque l'erreur totale du réseau est < 0,05 % à la ligne 57 de and.pde. Alternativement, l'apprentissage peut être programmé pour s'arrêter après un certain nombre d'époques en utilisant la ligne 55. Une fois l'apprentissage terminé, l'application parcourt simplement les entrées binaires dans l'ordre, permettant ainsi au réseau neuronal de montrer ce qu'il a appris (figure 3).
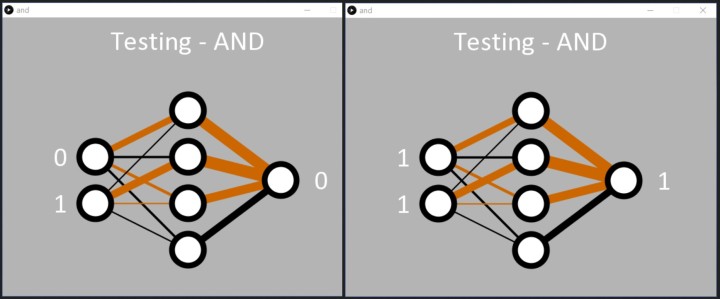
les quatre combinaisons d'entrées binaires et affiche la réponse de sortie du réseau.
Dans la console texte, les entrées sont affichées (sous la forme d'une valeur décimale comprise entre 0 et 3) avec la sortie calculée au format texte, comme suit :
0 : 5.2220514E-4
1 : 0.038120847
2 : 0.04245576
3 : 0.94188505
0 : 5.2220514E-4
1 : 0.038120847
2 : 0.04245576
3 : 0.94188505
Pour ceux qui sont intéressés, l'erreur de sortie pour les entrées appliquées et l'erreur moyenne du réseau sont écrites toutes les 50 époques dans un fichier CSV nommé and-error.csv. Il est possible d'importer ce fichier dans Excel pour examiner comment le réseau a convergé vers la solution (figure 4). La sortie montre comment l'erreur oscille entre des valeurs élevées et faibles pour des combinaisons d'entrée/sortie spécifiques. Comme nous l'avons déjà vu, l'erreur élevée est probablement liée à la sortie des motifs '00', '01' et '10' qui est beaucoup trop haute pendant la première phase d'apprentissage. L'erreur faible est probablement due au fait que le réseau évalue l'entrée '11'.
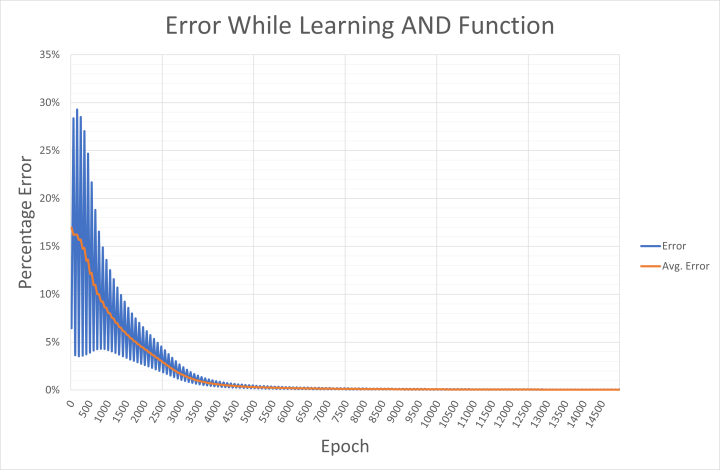
Ces erreurs de motifs individuels sont moyennées sur quatre époques pour calculer l'erreur moyenne du réseau. Si votre PC n'utilise pas la langue anglaise, vous pouvez remplacer le ',' dans le fichier CSV par un ';' comme séparateur, et ensuite le '.' par ',' dans un éditeur de texte (tel que Notepad++) avant d'effectuer une importation de données dans Excel.
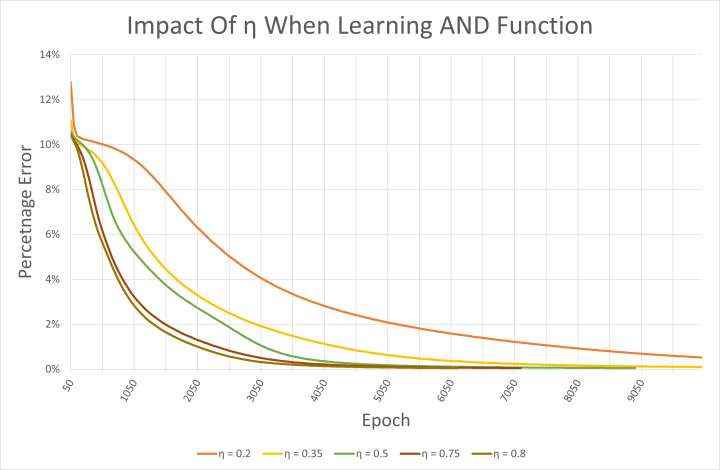
Le fichier CSV est également intéressant pour examiner l'impact du taux d'apprentissage sur le réseau. Le code de l'exemple utilise un taux d'apprentissage η de 0,5. Des nombres plus élevés permettent au réseau d'apprendre plus rapidement, comme on peut le voir sur la figure 5. Cependant, ils peuvent également provoquer des oscillations et aboutir à un réseau qui ne converge jamais vers le résultat d'apprentissage souhaité. Tous les taux d'apprentissage testés ici ont donné lieu à un réseau fonctionnant correctement et ayant appris la fonction ET. Il convient toutefois de noter que les poids de départ ont été choisis de manière aléatoire à chaque fois.
Le MLP peut-il apprendre la fonction OU exclusif ?
Le référentiel comprend également des exemples pour une fonction OU dans processing/or/or.pde. Etant linéairement séparable, le MLP n'a aucun problème à apprendre cette fonction non plus. Peut-être trouverez-vous utile d'examiner la différence des poids après l'apprentissage par rapport à l'exemple de la fonction ET. Les fichiers or.pde et and.pde peuvent être facilement modifiés pour apprendre au réseau les fonctions NON ET et NON OU. Cependant, le moment de vérité arrive avec la fonction OU exclusif.
Un exemple est proposé dans processing/xor/xor.pde qui fonctionne comme le code précédent et utilise la même configuration de nœuds MLP 2/4/1 (entrée/caché/sortie) (figure 6). Avec le taux d'apprentissage appliqué (η = 0,5), il faudra probablement 15 000 époques ou plus avant que la sortie ne commence à changer. Environ 35 000 époques sont nécessaires avant que l'erreur moyenne cible de 0,05 % soit atteinte.
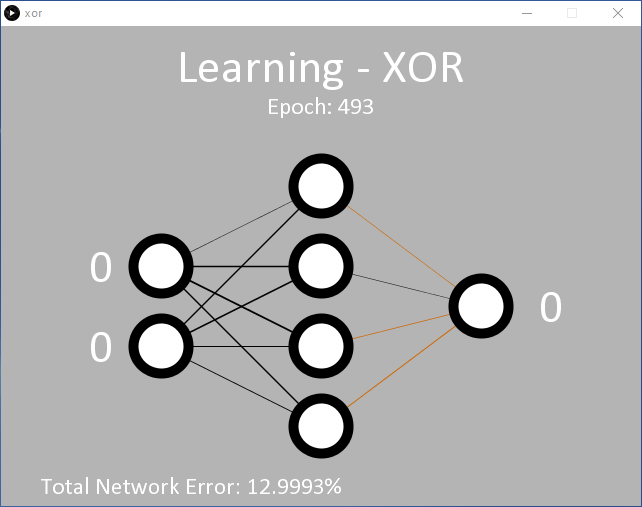
le MLP montre qu'il a des difficultés à trouver les poids appropriés.
Et il est clair que le réseau a du mal à apprendre la fonction OU exclusif. Cela se reflète dans les poids affichés qui oscillent entre positif et négatif avant de choisir une direction, et l'erreur du réseau diminue très progressivement. Cela s'explique par le fait que '00' et '11' (représentés par 0,01 et 0,01, et 0,99 et 0,99 sur les entrées) sont tous deux censés donner une sortie à 0,01. Mathématiquement, des valeurs d'entrée de 0,99 entraînent des valeurs de sortie élevées jusqu'à ce que le réseau soit capable de faire baisser le résultat vers 0,01 pendant l'apprentissage. Cela se voit dans l'erreur de sortie enregistrée dans xor-error.csv au cours de l'apprentissage (figure 7).
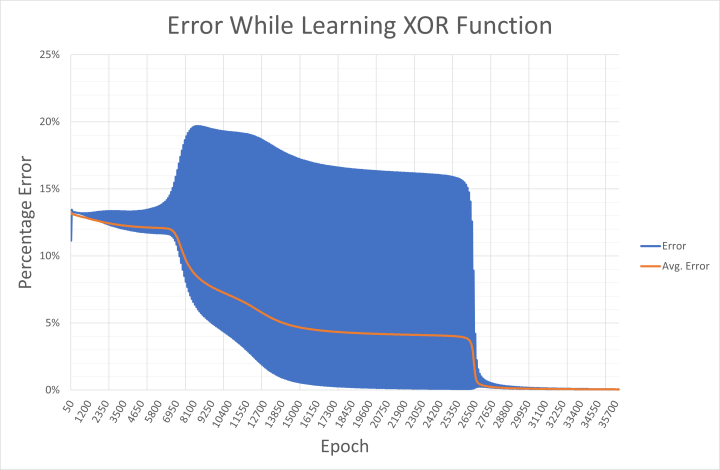
Malgré les difficultés de la tâche, le réseau apprend la fonction OU exclusif comme demandé. Une fois que l'erreur est inférieure à 0,05 %, le code Processing applique consciencieusement les entrées binaires au réseau, et la sortie répond en détectant correctement les modèles '01' et '10'. Le code affiche alors un 1 sur le nœud de sortie (figure 8).
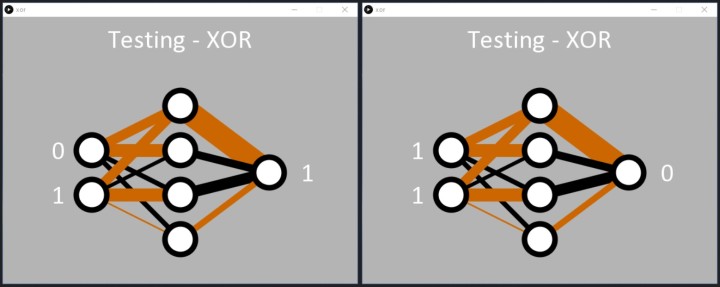
Comme avec le code ET, nous pouvons voir comment le réseau a appris la fonction OU exclusif. Deux nœuds cachés possèdent une ligne noire et brune entrante, et une ligne noire épaisse sortante (deux nœuds du milieu de la figure 8). Ils semblent être responsables de la classification '01' et '10'. Le réseau a également très bien résolu le passage de '00' en entrée à '0' en sortie (nœud caché supérieur). À cette occasion, l'entrée '11' semble être traitée par le nœud caché inférieur, mais il se peut qu'elle n'ait pas été très bien résolue pendant l'apprentissage, ce qui a entraîné une erreur plus élevée que souhaitée pour l'entrée '11'. Si l'on réexécute le code, il est probable qu'un nœud caché traite manifestement le '11' et que deux lignes noires entrent dans l'un des nœuds cachés (figure 9).
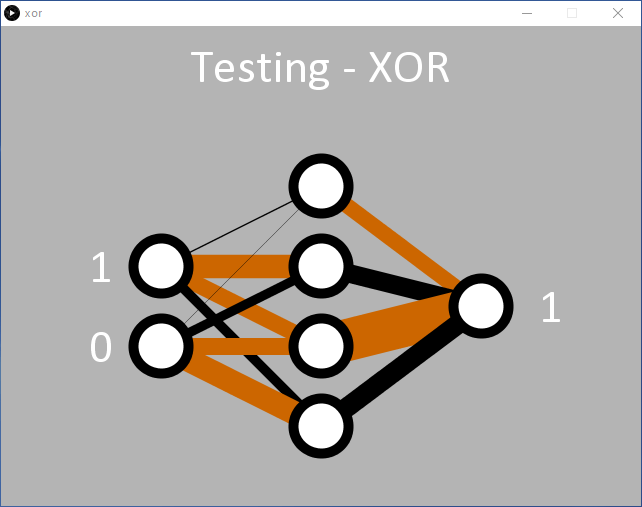
Et après ?
L'une des choses les plus importantes à retenir est peut-être qu'avec les réseaux neuronaux, il n'y a pas de bonne ou de mauvaise réponse. Le réseau lui-même ne fait que classer la probabilité selon laquelle les entrées que vous avez fournies correspondent aux entrées que vous recherchez. Si vous l'avez configuré, entraîné et qu'il donne le résultat souhaité, il est probablement correct. Idéalement, vous cherchez également à obtenir ce résultat avec un nombre minimal de nœuds pour économiser de la mémoire et du temps de calcul.
Bien que la visualisation soit agréable, elle n'est pas totalement nécessaire. Si vous souhaitez en savoir plus, vous pouvez modifier le projet processing/fsxor/fsxor.pde qui se passe des visualisations. La suppression du code qui écrit les valeurs d'erreur dans un fichier CSV accélère aussi considérablement le code. Vous pouvez ensuite écrire votre propre code en utilisant la classe Neural pour étudier les questions suivantes :
- Quel est l'impact du taux d'apprentissage sur le réseau lors de l'apprentissage de la fonction OU exclusif ? Vous pouvez également essayer les mêmes poids de départ à chaque fois.
- Pouvez-vous initialiser les poids avec des valeurs qui encouragent le réseau à un processus de résolution exigeant moins d'époques ? Examinez éventuellement les poids de sortie d'une session exécutée précédemment.
- De combien de nœuds cachés avez-vous besoin pour l'apprentissage de la fonction ET ? Combien en faut-il pour apprendre la fonction OU exclusif ? Est-il possible d'avoir trop de nœuds cachés ?
- Est-il judicieux d'avoir deux nœuds de sortie ? Le premier pourrait classer les modèles indésirables comme 0,99 (pour le OU exclusif, '00' et '11'), tandis que le second est utilisé pour classer les modèles souhaités comme 0,99 (pour le OU exclusif, '10' et '01').
Dans le prochain article sur les réseaux neuronaux, nous entraînerons le réseau neuronal à reconnaître les couleurs d'une webcam fixée à notre PC. Si vous le souhaitez, pourquoi ne pas développer et tester une configuration de nœuds MLP que vous pensez être à la hauteur de la tâche ?

Übergizmo, septembre 2016
Daddy’s Car, une chanson composée par intelligence artificielle : http://bit.ly/3shyfo6
Des questions ? Des commentaires ?
Avez-vous des questions ou des commentaires à propos de cet article ? Envoyez un courrier électronique à l'auteur à l'adresse stuart.cording@elektor.com.
Traduction: Pascal Godart


Discussion (0 commentaire(s))